Basic structure of a tensor
// ggml.h
struct ggml_tensor {
enum ggml_type type; // e.g. GGML_TYPE_F32
enum ggml_backend backend; // cpu or gpu
int n_dims; // ranges from 1 to 4
// number of elements
int64_t ne[GGML_MAX_DIMS];
// stride in bytes
size_t nb[GGML_MAX_DIMS];
enum ggml_op op; // either None or operations between tensors
struct ggml_tensor * src[GGML_MAX_SRC]; // empty or points to src tensors for OP
void * data; // tensor or null if tensor is an op
char name[GGML_MAX_NAME];
};-
necontains the number of elements in each dimension. ggml is row-major order, e.g. for a 2x4 matrix A (2 rows, 4 columns), each row has 4 elements, thusne[0] = 4andne[1] =2(number of elements in a column)- This means that the fastest moving dimension is the “first one”, which is the opposite of the Pytorch notation where the last one is the fastest moving.
-
nbcontains the stride: the number of bytes between consecutive elements in each dimension.- assuming float32,
nb[0] = sizeof(float) = 4 - Then,
nb[1] = ne[0]*nb[0](length of first dim in bytes) - We can then define bottom-up:
nb[i]=ne[i-1]*nb[i-1]- (4,3,2) tensor
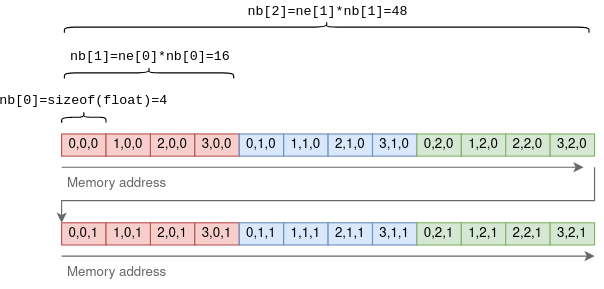
- (4,3,2) tensor
- assuming float32,
Tensors operations and views
-
opmay be any supported operation between tensors. Setting it toGGML_OP_NONEmarks that the tensor holds data. Other values can mark an operation. This is because ggml_tensors are part of a computation graph. -
srcis an array of pointers to the tensors between which the operation is to be taken. For example, ifop == GGML_OP_MUL_MAT, thensrcwill contain pointers to the two tensors to be multiplied. Ifop == GGML_OP_NONE, thensrcwill be empty. -
datapoints to the actual tensor’s data, orNULLif this tensor is an operation. It may also point to another tensor’s data, and then it’s known as a view e.g.ggml_transpose(). -
Matmul example (
resultdoes not contain any data. It just represents the theoretical result of multiplying a and b)
// ggml.c (simplified and commented)
struct ggml_tensor * ggml_mul_mat(
struct ggml_context * ctx,
struct ggml_tensor * a,
struct ggml_tensor * b) {
// Check that the tensors' dimensions permit matrix multiplication.
GGML_ASSERT(ggml_can_mul_mat(a, b));
// Set the new tensor's dimensions
// according to matrix multiplication rules.
const int64_t ne[4] = { a->ne[1], b->ne[1], b->ne[2], b->ne[3] };
// Allocate a new ggml_tensor.
// No data is actually allocated except the wrapper struct.
struct ggml_tensor * result = ggml_new_tensor(ctx, GGML_TYPE_F32, MAX(a->n_dims, b->n_dims), ne);
// Set the operation and sources.
result->op = GGML_OP_MUL_MAT;
result->src[0] = a;
result->src[1] = b;
return result;
}Computing tensors
- The
ggml_mul_mat()function above, or any other tensor operation, does not calculate anything but just prepares the tensors for the operation. - A different way to look at it is that it builds up a computation graph where each tensor operation is a node,
- The operation’s sources are the node’s children.
- In the matrix multiplication scenario, the graph has a parent node with operation
GGML_OP_MUL_MAT, along with two children.
// llama.cpp
static struct ggml_cgraph * build_graph(/* ... */) {
// ...
// A,B are tensors initialized earlier
struct ggml_tensor * AB = ggml_mul_mat(ctx0, A, B);
}In order to actually compute the result tensor, the following steps are taken:
- Data is loaded into each leaf tensor’s
datapointer. In the example the leaf tensors areAandB. - The output tensor (
AB) is converted to a computation graph usingggml_build_forward(). This function is relatively straightforward and orders the nodes in a depth-first order.1 - The computation graph is run using
ggml_graph_compute(), which runsggml_compute_forward()on each node in a depth-first order.ggml_compute_forward()does the heavy lifting of calculations. It performs the mathematical operation and fills the tensor’sdatapointer with the result. - At the end of this process, the output tensor’s
datapointer points to the final result.