-
A tensor is a mathematical concept. But to represent it on our computers, we have to define some sort of physical representation for them.
-
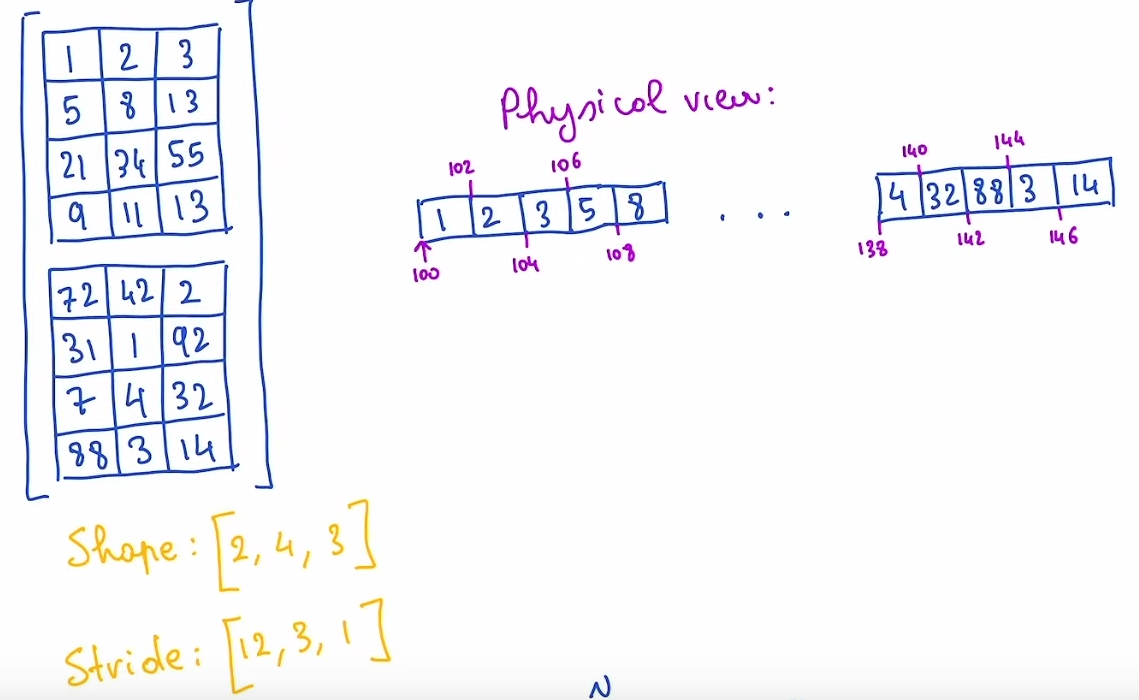
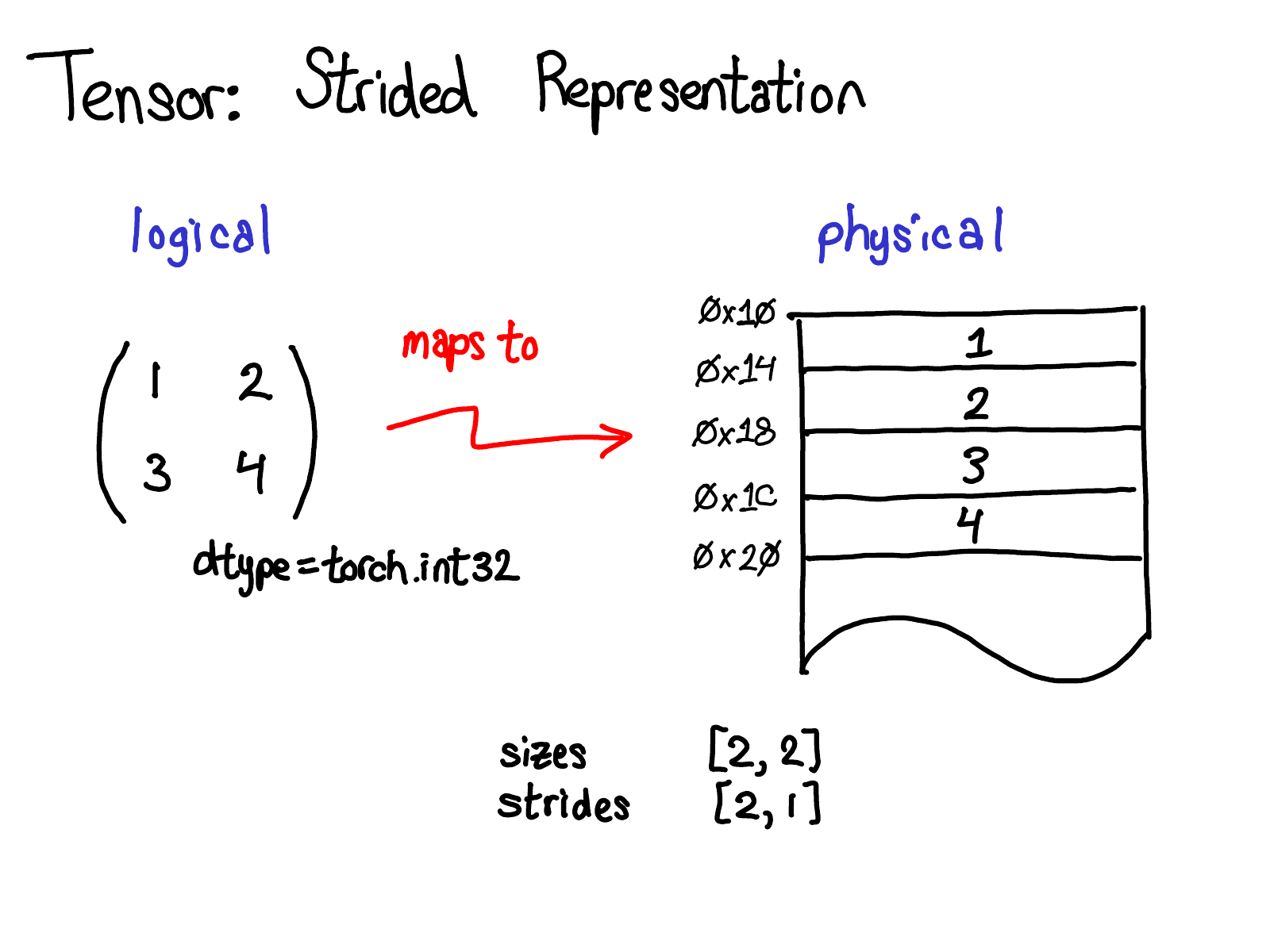
The most common representation is to lay out each element of the tensor contiguously in memory (that’s where the term contiguous comes from), writing out each row to memory, as you see above.
Example (2D Matrix)
- In the example below, the tensor contains 32-bit integers, so you can see that each integer lies in a physical address, each offset four bytes from each other.
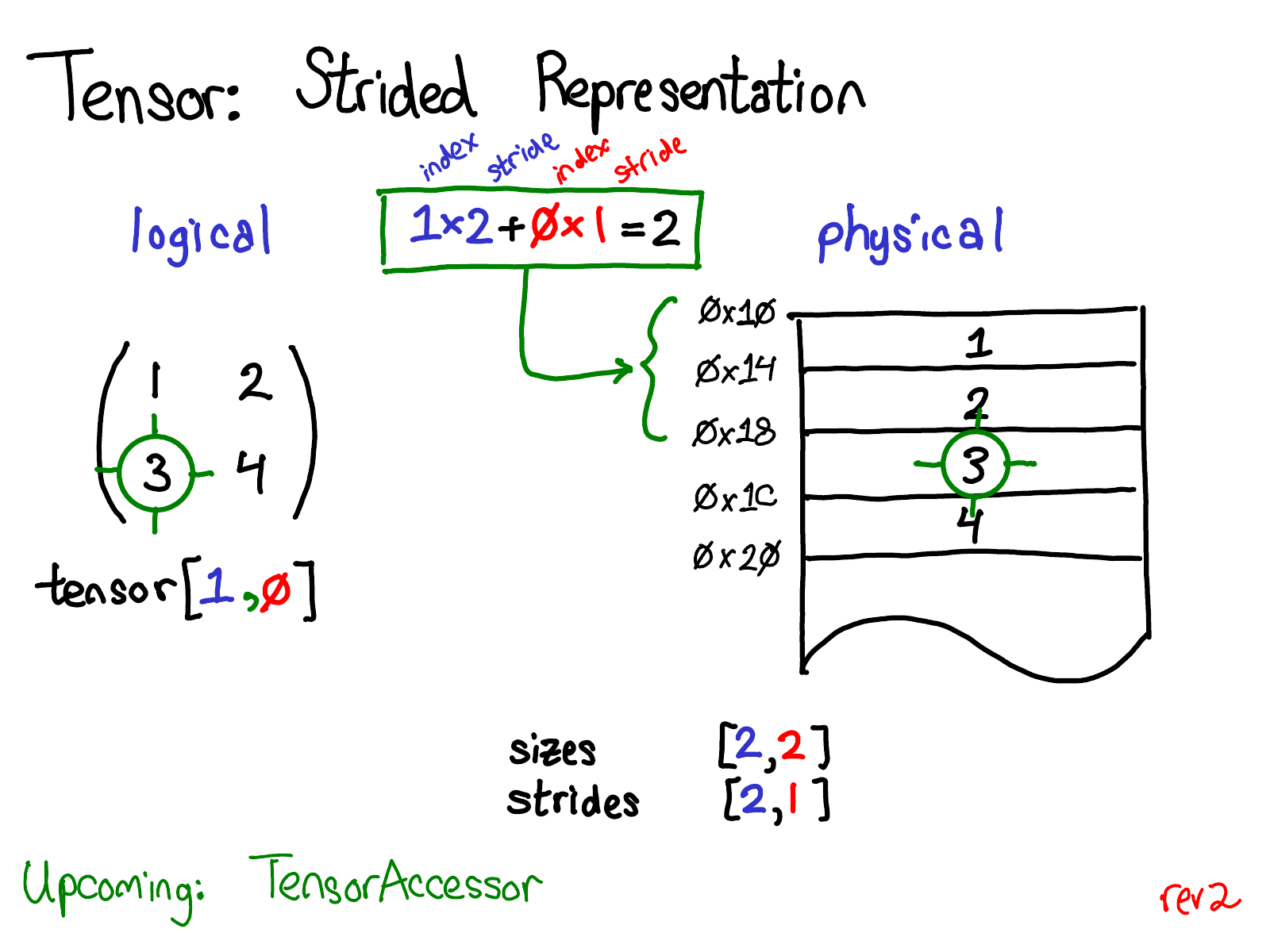
- To remember what the actual dimensions of the tensor are, we have to also record what the sizes are as extra metadata.
- This layout is called row-major layout
- This means that elements within a row are stored in adjacent memory locations
- i.e. loading a row is cache friendly
- Rows are stored one after another in memory
- This usually results in a stride of the form
[row_size,1]
- This means that elements within a row are stored in adjacent memory locations
- A column-major layout will have a stride of the form
[1,col_size]
Example (2D Matrix transpose)
- A transpose is just a swap of the strides
- i.e.
x.transpose(1,0)means `new_stride[0]=stride[1], new_stride[1]=stride[0]
- i.e.
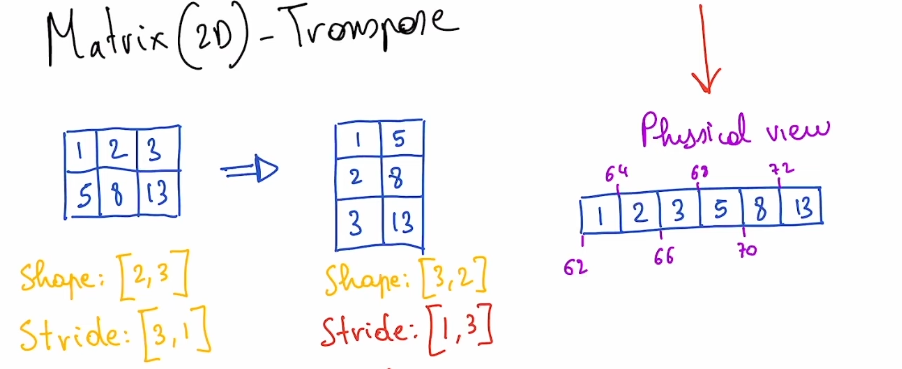
- In this example, the tensor is no longer contiguous (at least according to row-major layout, which assumes elements within a row are stored in adjacent memory locations)
- Side note: this means that, in PyTorch, you can not call
.view()on a transposed tensor, as it no longer satisfies the “contiguous property” , you need to callreshape, which will reallocate the tensor in a contiguous manner in the physical layout
- Side note: this means that, in PyTorch, you can not call
Defining the strides i.e. how do you know if a tensor is contiguous?
- When a tensor of dimension is allocated with a given
shape:list[int], it is allocated in a contiguous manner (row-major) and the stride is defined as:- `stride = torch.cumprod(shape[::-1][:-1])[::-1]
- If a tensor’s stride doesn’t satisfy this property, it is not considered contiguous.